Representation of integers
- From binary to decimal
- From decimal to binary
Representation of text
Strings
- search/replace a substring within a string
- splitting a strings at delimiters
Interactive input from the command line:
Reading and writing to text files
Counting lines and words in a text file.
Representation of images
Grey level pictures
- Colored bitmaps

Representation of integers

There are 10 kinds of people: those who count in binary and the others.

Computers represent everything as series of 0 and 1, also known as bits (for “binary digits”).

Just like a number can be written in base 10, it can be written in base 2 (or in any other base):

12 = 10  + 2 = 1.(10^1) + 2.(10^0) 
12 = 8 + 4 = 2^3 + 2^1 => 1010

33 = 30  + 3 = 3.(10^1) + 3.(10^0)
33 = 32 + 1 = 2^5 + 2^0 => 100001

The binary representions of the first integers:

Remember that a number represented by four digits “d3 d2 d1 d0” in a basis ‘b’, has a value of d3b^3 + d2b^2 + d1b^1 + d0b^0

In binary, there are only two possibilities for the digits: {0,1}
In decimal, 10 possible characters
In hexadecimal, 16 possible characters 0-9, A, B, C, D, E, F (D8F1 = 1416^3 + 810^2 + 1516^1 + 116^0)

To learn more about how integer numbers are represented in binary format, you can check out http://csunplugged.org/binary-numbers

Convert (manually) into decimal the following binary numbers:

101
1000
1011
11111111

. . .

Answer: 5, 8, 11, 255

From binary to decimal

Let us write a function that, given the binary representation of a number as a string of ‘0’ and ‘1’, returns its value as a integer.

Let us first suppose that we want to convert a string containing exactly 8 binary digits (e.g. ‘01011010’) into decimal. How would you do that?

. . .

def todec8bits(s):
    return int(s[0])*128 + int(s[1])*64 + int(s[2])*32 + \
           int(s[3])*16 + int(s[4])*8 + int(s[5])*4 + \
           int(s[6])*2 + int(s[7])

todec8bits("01010101")

One issue with this code:

todec8bits("0101010")
todec8bits("010101010")

Remark: on your computers, integers are represented either as 32 or 64 bits, depending on your processor/operating system.

Why is this is relevant: suppose you perform an EEG recording with 256 electrodes every milliseconds for one hour. How large is the data?

Beware: your computer can make mistakes if you add too large numbers!!!

Another solution demonstrating several new Pythonic constructions that we have not seen yet:

pow2 = [2 ** n for n in range(7, -1, -1)]
n = 0
for b, p in zip(s, pow2):
    n += int(b) * p
print(n)

. . .

We could modify it to adapt to the size of the string ‘s’.

My favorite which has the advantage of working with strings of unlimited size:

def todec(s):
    """ convert a string of 0 and 1 representing a binary number into an integer """
    n = 0
    for b in s:
        n = n * 2 + int(b)
    return n

for i in ['101', '1000', '1011', '11111111']:
    print(todec(i))

From decimal to binary

Now we will go in the other direction: Our aim is to write a program that, given a number (in decimal), computes its binary representation.

If you have an idea how to program it, please proceed. If not, we propose that you follow the following steps:

Study the program below. Execute it with various values of the variable num. Do you understand the last line? Do you see a limitation of this program?

num = 143
d3 = int(num/1000) % 10 # thousands
d2 = int(num/100)  % 10 # hundreds
d1 = int(num/10)   % 10 # dec
d0 =  num % 10
print(str(d3) + str(d2) + str(d1) + str(d0))

Adapt the above program to print the binary representation of num

. . .

num = 17
b0 = num % 2
b1 = int(num/2) % 2
b2 = int(num/4) % 2
b3 = int(num/8) % 2
b4 = int(num/16)  % 2
b5 = int(num/32)  % 2
b6 = int(num/64)  % 2
b7 = int(num/128) % 2
b8 = int(num/256) % 2
print(str(b8) + str(b7) +  str(b6) + str(b5) + str(b4) + str(b3) + str(b2) + str(b1) + str(b0))

. . .

Modify the above program to print the binary representations of every number between 0 and 255.

. . .

def tobin(num):
    b7 = int(num/128) % 2
    b6 = int(num/64)  % 2
    b5 = int(num/32)  % 2
    b4 = int(num/16)  % 2
    b3 = int(num/8) % 2
    b2 = int(num/4) % 2
    b1 = int(num/2) % 2
    b0 = num % 2
    return (str(b7) +  str(b6) + str(b5) + str(b4) + \
            str(b3) + str(b2) + str(b1) + str(b0))

for n in range(256):
    print(n, tobin(n))

. . .

(Advanced) Write an improved version that uses a loop and does not have a limitation in size.

. . .

def binary(n):
    if n==0:
        return "0"
    s = ""
    while n > 0:
        b = str(n % 2)
        s = b + s
        n = n / 2
    return s

. . .

Study the following code. Do you understand why it works?

def binary(num):
    if num == 0:
        return "0"
    if num == 1:
        return "1"
    return(binary(int(num /2)) + binary(num % 2))

print(binary(1234))

. . .

Answer: It is a recursive function which calls itself. See http://en.wikipedia.org/wiki/Recursion_%28computer_science%29

. . .

Remark: measures of memory size

1 byte = 8 bits
1 Kilobyte (KB) = 1024 bytes
1 Megabyte (MB) = 1024 kbytes = 1048576 bytes
1 Gigabytes (GB) = 1024 Mbytes
Terabyte, Petabyte, Exabyte…

Exercice (advanced): Write a function that return the hexadecimal representation (base 16) of a number.

To go further:

If you want to know how negative integer numbers are represented, see http://en.wikipedia.org/wiki/Two%27s_complement
To understand how real numbers are encoded, read What Every Programmer Should Know About Floating-Point Arithmetic and https://docs.python.org/2/tutorial/floatingpoint.html#tut-fp-issues

Representation of text

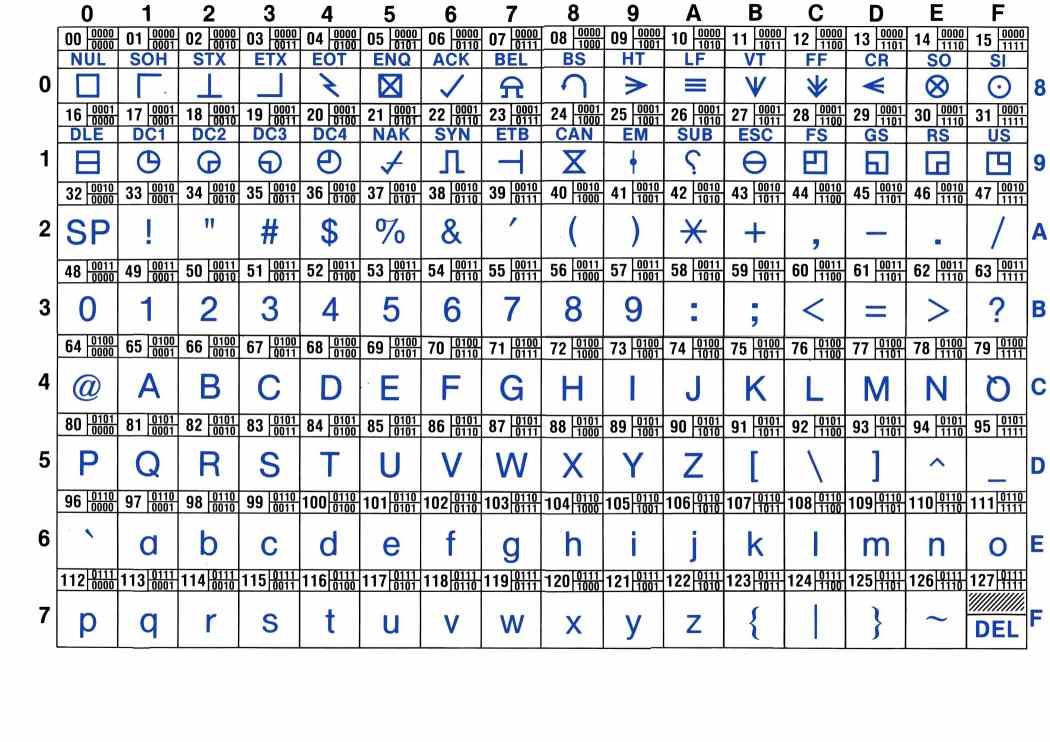
A text file is nothing but a sequences of characters.

For a long time, characters were encoded using ASCII code.

ascii table

In Python, you can know the code of a character with the function ord:

print(ord('a'))
print(ord('@'))

The inverse of ord is chr.

lookup the ASCII representation of your first name in the table and use the chr function of Python to print it.

. . .

For example, if you name is ‘ZOE’, you would type:

print(chr(90)+chr(79)+chr(69))

Remark: ASCII codes use one byte (=8bits) per character. This is fine for English, but cannot cover all the caracters of all alphabets. It cannot even encode french accented letters.

Unicode was invented that associate a unique 2 bytes number to each character of any human script. It is possible to write text files using these number, but more economic to encode the most common letters with one byte, and keep the compatibility with ASCII (UTF-8).

print("".join([unichr(c) for c in range(20000, 21000)]))

Strings

In Python, text can be stored in objects called strings.

String constants are enclosed between single quotes

'Bonjour le monde!'

Or double quotes

"Bonjour le monde !"

Or “triple” quotes for multilines strings

"""
Bonjour le monde!

Longtemps je me suis levé de bonne heure,
Les sanglots longs des violons,
...
"""

They have a type ‘str’.

>>> type('bonjour')
<type 'str'>

To convert an object to a string representation:

str(10)
a = dict((("a",1), ("b",2)))
str(a)

A string is nothing but a sequence of characters.

a = 'bonjour'
print(a[0])
print(a[1])
print(a[2])
print(a[2:4])
print(len(a))

for c in 'bonjour':
    print(c)

Operations on strings

a = 'bonjour'
b = 'hello'
a + b
a + ' ' + b

A set of functions to manipulate strings is available in the module ‘string’.

import string
string.upper(a)
string.lower('ENS')

search/replace a substring within a string

a = 'alain marie jean marc'
a.find('alain')
a.find('marie')
a.find('ma')
a.find('marc')
a.find('o')

a.replace('marie','claude')
a

splitting a strings at delimiters

a = 'alain marie jean marc'
a.split(" ")

Read (see https://docs.python.org/2/library/string.html) to learn about more string functions.

Interactive input from the command line:

name = raw_input('Comment vous appelez-vous ? ')

print "Bonjour " + name + '!'

Reading and writing to text files

With Atom, create a text file containing a few lines of arbitrary content, an save it under the filename ‘test.txt’
with ipython running in the same directory where you saved test.txt

f = file('test.txt')
o = f.read()
print(o)
lines = o.split("\n")
print(lines)

Counting lines and words in a text file.

Download Alice in Wonderland

f = file('alice.txt')
o = f.read()
print(o)
lines = o.split("\\n")
print(lines)

Write a program that counts the number of lines, and number of words in alice.txt (we suppose that words are separated by spaces).

. . .

f = file('alice.txt')
o = f.read()
print(o)
lines = o.split("\n")

nlines = len(lines)

nw = 0
for l in lines:
    nw += len(l.split(" "))

print(nlines)
print(nw)

Write a program that detects if a text file contains the word ‘NSA’

. . .

def spot_nsa(filename):
    f = file(filename)
    o = f.read()
    lines = o.split("\n")
    found = False
    for l in lines:
        if "NSA" in l.split(" "):
            found = True
            break
    return found

Representation of images

Images can be stored either:

as bitmaps, that is a two dimensional arrays of dots (formats: bmp, png, gif, jpeg…)
as vectorized formats, the image contain instruction for drawing objects (eps, pdf, svg, …).

Here we are just going to manipulate bitmaps.

Each dot (pixel) is either ‘0’ (black) or ‘1’ (white).

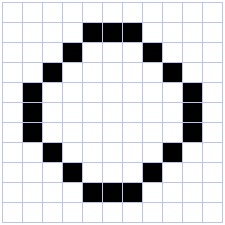
What is the size in kilobytes of a 1024x768pixels black and white image ?

. . .

Answer: 1024*768/8/1024=96 KB

Execute the following code in ipython:

import numpy as np
import matplotlib.pyplot as plt

a = np.array([[0, 0, 0, 0, 0, 0, 0],
              [0, 0, 1, 1, 1, 0, 0],
              [0, 0, 1, 1, 1, 0, 0],
              [0, 0, 1, 0, 1, 0, 0],
              [0, 0, 1, 1, 1, 0, 0],
              [0, 0, 1, 1, 1, 0, 0],
              [0, 0, 0, 0, 0, 0, 0]])
plt.imshow(a, cmap=plt.cm.gray, interpolation='nearest')
plt.show()

Numpy’s arrays are a new type of object. There are similar to lists, but optimised for mathematical computations. Notably, they can be multidimensional (i.e. you can use a[i,j] notation). You can learn more about arrays in the documents http://www.pallier.org/cours/AIP2013/python4science.pdf and http://wiki.scipy.org/Tentative_NumPy_Tutorial.

Here is another example:

. . .

a = np.zeros((200,200))
for i in range(200):
    a[i, i] = 1
plt.imshow(a, cmap=plt.cm.gray, interpolation='nearest')
plt.show()

a[0:200:2,] = 1
plt.imshow(a, cmap=plt.cm.gray, interpolation='nearest')
plt.show()

Grey level pictures

Each dot is now associated to an integer value, e.g. ranging from 0 to 255 for 8-bits codes, coding for a grey level (smaller=darker). Each dot needs one byte.

How large is the file for an image 1024x768 pixels with 256 grey levels?

The following code displays an image:

import scipy.misc
l = scipy.misc.lena()
plt.imshow(l,  cmap=plt.cm.gray)
plt.show()

This code runs a low pass (averaging) filter on it:

import scipy.ndimage
bl = scipy.ndimage.gaussian_filter(l, 3)
plt.imshow(bl,  cmap=plt.cm.gray)
plt.show()

Edge detector It is easy to implement an edge detector with a neural network. See https://courses.cit.cornell.edu/bionb2220/UnderstandingLateralInhibition.html.

Using the ndimage.convolve function, apply the following filters to the image and diplay the results.

kernel1 = np.array([[-1, -1, -1],
                   [-1,  8, -1],
                   [-1, -1, -1]])

bl=scipy.ndimage.convolve(l,kernel1)
plt.imshow(bl,  cmap=plt.cm.gray)
plt.show()


kernel2 = np.array([[-1, -1, -1, -1, -1],
                   [-1,  1,  2,  1, -1],
                   [-1,  2,  4,  2, -1],
                   [-1,  1,  2,  1, -1],
                   [-1, -1, -1, -1, -1]])
bl=scipy.ndimage.convolve(l,kernel2)
plt.imshow(bl,  cmap=plt.cm.gray)
plt.show()

More manipulations are available at http://scipy-lectures.github.io/advanced/image_processing/.

Colored bitmaps

Each dot is now associated to three bytes, representing the Red, Gree and Blue intensities (see http://www.colorpicker.com/).

How large is the file for a 1024x768 RGB image?

Exercice: What are the RGB triplets for BLACK, WHITE, RED, YELLOW?

How numbers, images and texts are represented in the computer

Christophe@pallier.org

Sept. 2015

Representation of integers

From binary to decimal

From decimal to binary

Representation of text

Strings

search/replace a substring within a string

splitting a strings at delimiters

Interactive input from the command line:

Reading and writing to text files

Counting lines and words in a text file.

Representation of images

Grey level pictures

Colored bitmaps